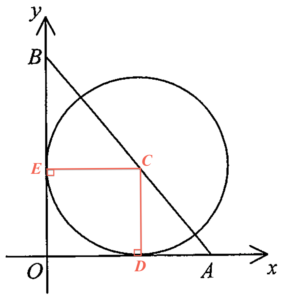
Denote $C$ the centre of the circle. Let $D$ and $E$ be the points of contact of $OA$ and $OB$ respectively. Let $r$ be the radius. Note that $CD = CE = OE = OD = r$. Note also that the coordinates of $C$ are $(r,r)$. Since the coordinates of $A$ are $(21,0)$, then $OA = 21$. And Since the coordinates of $B$ are $(0,28)$, then $OB=28$ and $BE = 28 -r$. Note that $\Delta OAB \sim \Delta ECB$, then we have
$\begin{array}{rcl}
\dfrac{OA}{EC} & = & \dfrac{OB}{EB} \\
\dfrac{21}{r} & = & \dfrac{28}{28-r} \\
21(28-r) & = & 28r \\
588 – 21r & = & 28r \\
49r & = & 588 \\
r & = & 12
\end{array}$
Therefore, the radius is $12$ and the coordinates of the centre are $(12,12)$. Hence, the equation of the circle
$\begin{array}{rcl}
(x-12)^2 + (y-12)^2 & = & 12^2 \\
x^2 -24x +144 + y^2 -24y + 144 & = & 144 \\
x^2 +y^2 -24x – 24y +144 & = & 0
\end{array}$

