2018-I-19

$\begin{array}{rcl}
(x-8)^2 + (y-2)^2 & = & r^2
\end{array}$

Consider

$\left\{\begin{array}{ll}
(x-8)^2 + (y-2)^2 = r^2 & \ldots \unicode{x2460} \\
kx – 5y – 21 = 0 & \ldots \unicode{x2461}
\end{array}\right.$

From $\unicode{x2461}$, we have

$\begin{array}{rcl}
kx – 5y – 21 & = & 0 \\
5y & = & kx – 21 \\
y & = & \dfrac{kx – 21}{5}\ \ldots \unicode{x2462}
\end{array}$

Sub. $\unicode{x2462}$ into $\unicode{x2460}$, we have

$\begin{array}{rcl}
(x-8)^2 + (\dfrac{kx -21}{5} – 2)^2 & = & r^2 \\
x^2 -16x + 64 + \left(\dfrac{kx-21}{5}\right)^2 – \dfrac{4(kx-21)}{5} + 4 – r^2 & = & 0 \\
25x^2 -400 x + 1600 + k^2x^2 -42kx + 441 -20kx +420 + 100 – 25r^2 & = & 0 \\
(k^2 + 25)x^2 + (-400 – 62k)x + (2561 -25r^2) & = & 0
\end{array}$

Since $L$ is a tangent to $C$, we have

$\begin{array}{rcl}
\Delta & = & 0 \\
(-400 – 62k)^2 – 4(k^2 + 25)(2561 – 25r^2) & = & 0 \\
4(k^2 + 25)(2561 – 25r^2) & = & (-400 – 62k)^2 \\
2561 – 25r^2 & = & \dfrac{(400 + 62k)^2}{4(k^2 + 25)} \\
25r^2 & = & 2561 – \dfrac{(200 + 31k)^2}{k^2 + 25} \\
r^2 & = & \dfrac{2561k^2 + 64025 – 40000 – 12400k – 961k^2}{25(k^2 + 25)} \\
r^2 & = & \dfrac{64k^2 – 496k + 961}{k^2 + 25}
\end{array}$

1. Note that $L$ passes through $D$. Therefore, we have

   $\begin{array}{rcl}
   k(18) – 5(39) – 21 & = & 0 \\
   18k & = & 216 \\
   k & = & 12
   \end{array}$

   Sub. $k=12$ into the result of (a), we have

   $\begin{array}{rcl}
   r^2 & = & \dfrac{64k^2 – 496k + 961}{k^2 + 25} \\
   r^2 & = & \dfrac{64(12)^2 – 496(12) + 961}{(12)^2 + 25} \\
   r^2 & = & 25 \\
   r & = & 5
   \end{array}$

2. Sketch the graph below according to the information of the question.
   

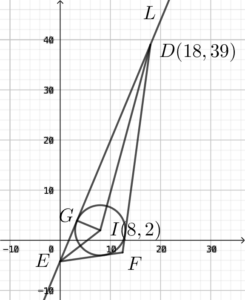
   Note that the $y$ intercept of $L$ is $\dfrac{-21}{5}$. Then, the coordinates of $E$ are $(0, \dfrac{-21}{5})$.

   Let $I(8,2)$ be the centre of $C$. Note that $I$ is the in-centre of $\Delta DEF$.

   Consider $\Delta DGI$. Note that $GI$ is a radius of the circle and $\angle IGD = 90^\circ$.

   $\begin{array}{rcl}
   DI & = & \sqrt{(18-8)^2 + (39-2)^2} \\
   DI & = & \sqrt{1469}
   \end{array}$

   Therefore, we have

   $\begin{array}{rcl}
   \sin \angle EDI & = & \dfrac{IG}{DI} \\
   \sin \angle EDI & = & \dfrac{5}{\sqrt{1469}} \\
   \angle EDI & = & 7.495\ 857\ 64^\circ
   \end{array}$

   Since $I$ is the in-centre of $\Delta DEF$, then we have

   $\begin{array}{rcl}
   \angle EDF & = & 2 \times \angle EDI \\
   \angle EDF & = & 14.991\ 715\ 28^\circ
   \end{array}$

   Consider $\Delta EGI$. Note that $GI$ is a radius of the circle and $\angle IGE = 90^\circ$.

   $\begin{array}{rcl}
   EI & = & \sqrt{(0-8)^2 + (\dfrac{-21}{5}-2)^2} \\
   EI & = & \dfrac{\sqrt{2561}}{5}
   \end{array}$

   Therefore, we have

   $\begin{array}{rcl}
   \sin \angle DEI & = & \dfrac{IG}{EI} \\
   \sin \angle DEI & = & \dfrac{5}{\frac{\sqrt{2561}}{5}} \\
   \angle DEI & = & 29.604\ 450\ 75^\circ
   \end{array}$

   Since $I$ is the in-centre of $\Delta DEF$, then we have

   $\begin{array}{rcl}
   \angle DEF & = & 2 \times \angle DEI \\
   \angle DEF & = & 59.208\ 901\ 49^\circ
   \end{array}$

   Therefore, $\angle DFE$

   $\begin{array}{cl}
   = & 180^\circ -\angle EDF – \angle DEF \\
   = & 180^\circ – 14.991\ 715\ 28^\circ – 59.208\ 901\ 49^\circ \\
   = & 105.799\ 383\ 2^\circ \\
   > & 90^\circ
   \end{array}$

   Therefore, $\Delta DEF$ is an obtuse-angled triangle.