2020-II-22

答案：C
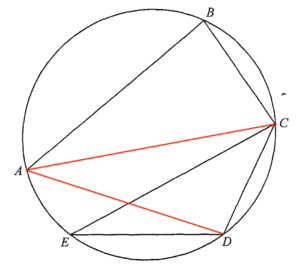
連結 $AC$ 及 $AD$。

考慮 $\Delta ABC$。由於 $\angle ABC = 90^\circ$，則 $AC$ 為圓的一直徑。

在 $\Delta ABC$ 運用畢氏定理，可得

$\begin{array}{rcl}
AC^2 & = & 10^2 + 5^2 \\
AC^2 & = & 125 \\
AC & = & \sqrt{125}\text{ cm}
\end{array}$

考慮 $\Delta ACD$。

$\begin{array}{rcll}
\angle ADC & = & 90^\circ & \text{(半圓上的圓周角)} \\
\angle CAD & = & \angle CED & \text{(同弓形內的圓周角)} \\
\angle CAD & = & 40^\circ
\end{array}$

由此，可得

$\begin{array}{rcl}
\sin \angle CAD & = & \dfrac{CD}{AC} \\
\sin 40^\circ & = & \dfrac{CD}{\sqrt{125}} \\
CD & = & \sqrt{125} \times \sin 40^\circ \\
CD & = & 7.186\ 583\ 952 \\
CD & \approx & 7 \text{ cm}
\end{array}$