2020-II-39

答案：A
在圓 $CDE$ 加點 $F$。連結 $DF$ 及 $EF$。

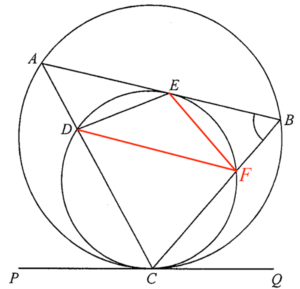
考慮 $\mathrm{\Delta }CDF$。

$\begin{array}{rcll}\mathrm{\angle }CDF& =& \mathrm{\angle }BCQ& \text{(內錯弓形的圓周角)}\\ \mathrm{\angle }CDF& =& {35}^{\circ }\end{array}$

由此，可得

$\begin{array}{rcll}\mathrm{\angle }ADE+\mathrm{\angle }EDF+\mathrm{\angle }CDF& =& {180}^{\circ }& \text{(直線上的鄰角)}\\ {100}^{\circ }+\mathrm{\angle }EDF+{35}^{\circ }& =& {180}^{\circ }\\ \mathrm{\angle }EDF& =& {45}^{\circ }\end{array}$

考慮 $\mathrm{\Delta }ABC$。

$\begin{array}{rcll}\mathrm{\angle }BAC& =& \mathrm{\angle }BCQ& \text{(內錯弓形的圓周角)}\\ \mathrm{\angle }BAC& =& {35}^{\circ }\end{array}$

考慮 $\mathrm{\Delta }ADE$。

$\begin{array}{rcll}\mathrm{\angle }ADE+\mathrm{\angle }AED+\mathrm{\angle }DAE& =& {180}^{\circ }& \text{(}\mathrm{\Delta }\text{ 的內角和)}\\ {100}^{\circ }+\mathrm{\angle }AED+{35}^{\circ }& =& {180}^{\circ }\\ \mathrm{\angle }AED& =& {45}^{\circ }\end{array}$

考慮 $\mathrm{\Delta }DEF$。

$\begin{array}{rcll}\mathrm{\angle }DFE& =& \mathrm{\angle }AED& \text{(內錯弓形的圓周角)}\\ \mathrm{\angle }DFE& =& {45}^{\circ }\end{array}$

由此，可得

$\begin{array}{rcll}\mathrm{\angle }DEF+\mathrm{\angle }EDF+\mathrm{\angle }EFD& =& {180}^{\circ }& \text{(}\mathrm{\Delta }\text{ 的內角和)}\\ \mathrm{\angle }DEF+{45}^{\circ }+{45}^{\circ }& =& {180}^{\circ }\\ \mathrm{\angle }DEF& =& {90}^{\circ }\end{array}$

考慮四邊形 $CDEF$。

$\begin{array}{rcll}\mathrm{\angle }DCF+\mathrm{\angle }DEF& =& {180}^{\circ }& \text{(圓內接四邊形的對角)}\\ \mathrm{\angle }DCF+{90}^{\circ }& =& {180}^{\circ }\\ \mathrm{\angle }DCF& =& {90}^{\circ }\end{array}$

由此，考慮 $\mathrm{\Delta }ABC$，可得

$\begin{array}{rcll}\mathrm{\angle }ABC+\mathrm{\angle }ACB+\mathrm{\angle }BAC& =& {180}^{\circ }& \text{(}\mathrm{\Delta }\text{ 的內角和)}\\ \mathrm{\angle }ABC+{90}^{\circ }+{35}^{\circ }& =& {180}^{\circ }\\ \mathrm{\angle }ABC& =& {55}^{\circ }\end{array}$