依題意略繪下圖。
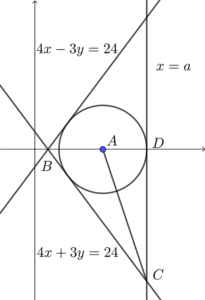
留意 $4x+3y=24$ 為 $4x-3y=24$ 對 $x$ 軸反射後所得的像。所以,該三角形為一等腰三角形,其中 $x$ 軸為對稱軸。故此,其內心在 $x$ 軸之上。
設 $A$ 為內心。則 $A$ 的坐標為 $(31,0)$。
把 $y=0$ 代入 $4x-3y=24$,可得
$\begin{array}{rcl}
4x – 3(0) & = & 24 \\
y & = & 6
\end{array}$
留意 $B$ 的坐標為 $(6,0)$。
把 $x=a$ 代入 $4x+3y=24$,可得
$\begin{array}{rcl}
4a + 3y & = & 24 \\
y & = & \dfrac{24-4a}{3}
\end{array}$
所以,$C$ 的坐標為 $(a, \dfrac{24-4a}{3})$。
留意 $D$ 的坐標為 $(a,0)$。
考慮 $\Delta BCD$。
$\begin{array}{rcl}
\tan \angle BCD & = & \dfrac{BD}{CD} \\
\tan \angle BCD & = & \dfrac{a-6}{0-\frac{24-4a}{3}} \\
\tan \angle BCD & = & \dfrac{3(a-6)}{4(a-6)} \\
\tan \angle BCD & = & \dfrac{3}{4} \\
\angle BCD & = & 36.869\ 897\ 65^\circ
\end{array}$
考慮 $\Delta ACD$。
$\begin{array}{rcl}
\tan \angle ACD & = & \dfrac{AD}{CD} \\
\tan \dfrac{36.869\ 897\ 65^\circ}{2} & = & \dfrac{a-31}{0-\frac{24-4a}{3}} \\
\dfrac{1}{3} & = & \dfrac{3(a-31)}{4a-24} \\
4a – 24 & = & 9(a-31) \\
4a – 24 & = & 9a – 279 \\
5a & = & 255 \\
a & = & 51
\end{array}$

