2017-II-40

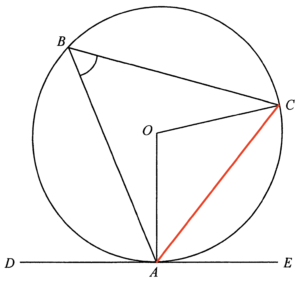
由於 $DE$ 為該圓於 $A$ 的切線，則

$\begin{array}{rcll}
\angle BCA & = & \angle BAD & \text{(內錯弓形的圓周角)}\\
\angle BCA & = & 68^\circ
\end{array}$

考慮 $\Delta OAC$。

$\begin{array}{rcl}
\angle OCA & = & \angle BCA – \angle BCO \\
\angle OCA & = & 68^\circ -26^\circ \\
\angle OCA & = & 42^\circ
\end{array}$

由於 $OA = OC$ (半徑)，則 $\angle OAC = \angle OCA$ (等腰 $\Delta$ 的底角)。由此，可得

$\begin{array}{rcll}
\angle AOC & = & 180^\circ – \angle OAC – \angle OCA & \text{($\Delta$ 的內角和)} \\
\angle AOC & = & 180^\circ – 42^\circ – 42^\circ \\
\angle AOC & = & 96^\circ
\end{array}$

由此，可得

$\begin{array}{rcll}
\angle ABC & = & \dfrac{1}{2} \times \angle AOC & \text{(圓心角兩倍於圓周角)} \\
\angle ABC & = & \dfrac{1}{2} \times 96^\circ \\
\angle ABC & = & 48^\circ
\end{array}$