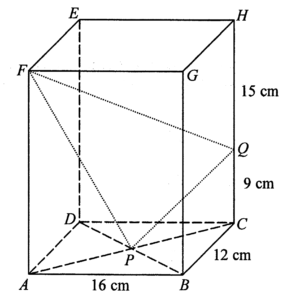
考慮 $\Delta ABC$,
$\begin{array}{rcl}
AC^2 & = & AB^2 + BC^2 \\
AC & = & \sqrt{16^2 + 12^2} \\
AC & = & 20\text{ cm}
\end{array}$
考慮 $\Delta QPC$,
$\begin{array}{rcl}
PQ^2 & = & QC^2 + PC^2 \\
PQ & = &\sqrt{9^2 + 10^2} \\
PQ & = & \sqrt{181} \text{ cm}
\end{array}$
考慮 $\Delta APF$,
$\begin{array}{rcl}
FP^2 & = & AP^2 + AF^2 \\
FP & = & \sqrt{10^2 + 24^2} \\
FP & = & 26\text{ cm}
\end{array}$
考慮 $\Delta FHQ$,
$\begin{array}{rcl}
FQ^2 & = & FH^2 + HQ^2 \\
FQ & = & \sqrt{20^2 + 15^2} \\
FQ & = & 25\text{ cm}
\end{array}$
考慮 $\Delta FPQ$,
$\begin{array}{rcl}
\cos \angle PFQ & = & \dfrac{FQ^2 + FP^2 – PQ^2}{2 (FQ)(FP)} \\
\cos \angle PFQ & = & \dfrac{25^2 + 26^2 – (\sqrt{181})^2}{2(25)(26)} \\
\cos \angle PFQ & = & \dfrac{56}{65} \\
\angle PFQ & = & 30.510\ 237\ 41^\circ \\
\sin \angle PFQ & = & \dfrac{33}{65}
\end{array}$

