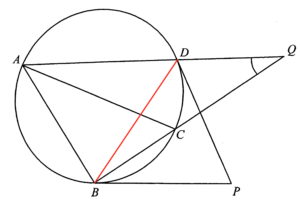
連接 $BD$。考慮 $\Delta PBD$,可得
$\begin{array}{rcll}
PD & = & PB & \text{(切線性質)} \\
\angle PDB & = & \angle PBD & \text{(等腰 $\Delta$ 的底角)} \\
\angle PDB & = & \dfrac{1}{2} \times (180^\circ – \angle AQB) & \text{($\Delta$ 的內角和)} \\
\angle PDB & = & \dfrac{1}{2} \times (180^\circ – 68^\circ) & \\
\angle PDB & = & 56^\circ
\end{array}$
考慮 $\Delta ABD$,可得
$\begin{array}{rcll}
\angle BAD & = & \angle PDB & \text{(內錯弓形的圓周角)} \\
\angle BAD & = & 56^\circ
\end{array}$
考慮 $\Delta ABQ$,
$\begin{array}{rcll}
\angle ABQ & = & 90^\circ & \text{(半圓上的圓周角)} \\
\angle AQB & = & 180^\circ – \angle BAD – \angle ABQ & \text{($\Delta$ 的內角和)} \\
\angle AQB & = & 180^\circ – 90^\circ – 56^\circ & \\
\angle AQB & = & 34^\circ
\end{array}$

