由於 $BD$ 為圓的一直徑,可得
$\begin{array}{ll}
BD\perp AB & \text{(半徑 $\perp$ 切線)}
\end{array}$
所以,$\angle EBA=90^\circ$。
在 $\Delta ABE$ 運用畢氏定理,可得
$\begin{array}{rcl}
AE^2 & = & AB^2 + BE^2 \\
10^2 & = & 6^2 + BE^2 \\
BE^2 & = & 64 \\
BE & = & 8 \text{ cm}
\end{array}$
留意
$\begin{array}{ll}
AC = AB & \text{(切線性質)} \\
AC = 6 \text{ cm}
\end{array}$
所以,$EC = 4 \text{ cm}$。
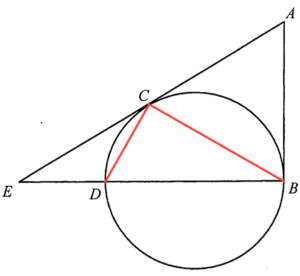
連結 $BC$ 及 $CD$。考慮 $\Delta BCE$ 及 $\Delta CDE$。
$\begin{array}{rcll}
\angle CEB & = & \angle DEC & \text{(公共角)} \\
\angle CBE & = & \angle DCE & \text{(內錯弓形內的圓周角)} \\
\angle BCE & = & 180^\circ – \angle CEB – \angle BCE & \text{($\Delta$ 的內角和)} \\
& = & 180^\circ \angle DEC – \angle DCE & \text{(已證)} \\
& = & \angle CDE & \text{($\Delta$ 的內角和)}
\end{array}$
所以,$\Delta BCE\sim \Delta CDE \text{ (A.A.A.)}$。
由此,可得
$\begin{array}{rcll}
\dfrac{BE}{CE} & = & \dfrac{CE}{DE} & \text{($\sim \Delta$ 的對應邊)} \\
\dfrac{8}{4} & = & \dfrac{4}{DE} \\
DE & = & 2 \text{ cm}
\end{array}$
所以,可得
$\begin{array}{rcl}
BD & = & BE – DE \\
& = & 8 – 2 \\
& = & 6 \text{ cm}
\end{array}$

