答案:A
由於 $AB=CD=EF$,三條弦 $AB$、$CD$ 及 $EF$ 與圓心 $O$ 的距離必為相等。由此,我們可畫出一個內接於 $\Delta PQR$ 的圓形,如下圖所示。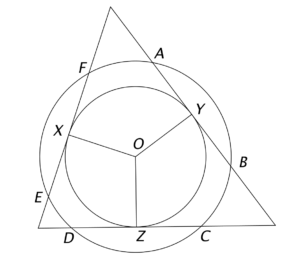
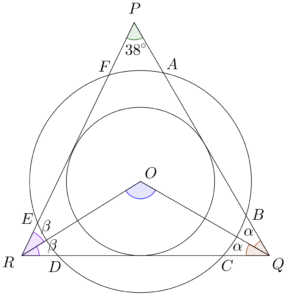
由於 $AB=CD=EF$,三條弦 $AB$、$CD$ 及 $EF$ 與圓心 $O$ 的距離必為相等。由此,我們可畫出一個內接於 $\Delta PQR$ 的圓形,如下圖所示。

留意 $PQ$、$QR$ 及 $PR$ 為小圓的切線,利用切線性質,可得
$\begin{array}{rcl}
\angle QOP & = & \angle OQR \\
\angle ORQ & = & \angle ORP
\end{array}$

考慮 $\Delta PQR$,可得
$\begin{array}{rcl}
2\alpha + 2\beta + 38^\circ & = & 180^\circ \\
\alpha + \beta & = & 71^\circ
\end{array}$
考慮 $\Delta ORQ$,可得
$\begin{array}{rcl}
\angle QOR & = & 180^\circ – \beta – \alpha \\
\angle QOR & = & 180^\circ – (\beta + \alpha) \\
\angle QOR & = & 180^\circ – 71^\circ \\
\angle QOR & = & 109^\circ
\end{array}$

