答案:C
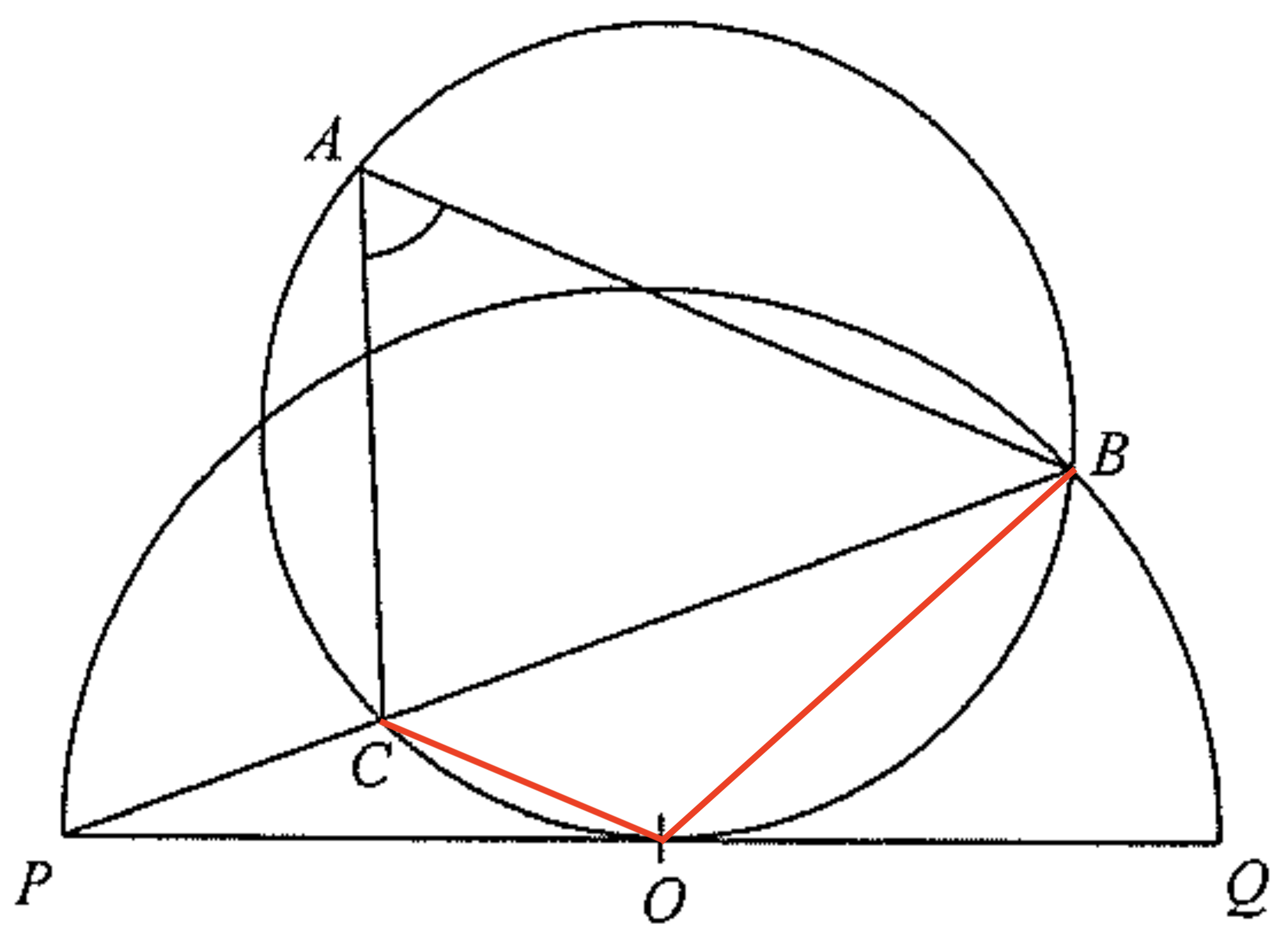

連結 $OB$。
$\begin{array}{rcl}
\angle BOQ & = & 2\times \angle BPQ \\
& = & 2\times 12^\circ \\
& = & 24^\circ
\end{array}$
在 $\Delta OBP$ 中,
$\because OB$ 及 $OP$ 均為半圓 $PBQ$ 的半徑,
$\therefore \angle OBP=\angle OPB=12^\circ$。
連結 $OC$。
$\because PQ$ 為圓 $ABC$ 在 $O$ 上的切線。
$\therefore \angle COP=\angle OBP = 12^\circ$。
由此,可得
$\begin{array}{rcl}
\angle BOC & = & 180^\circ – \angle BOQ-\angle COP \\
& = & 180^\circ-24^\circ-12^\circ \\
& = & 144^\circ
\end{array}$
因為 $ABOC$ 為圓內接四邊形,可得
$\begin{array}{rcl}
\angle BAC & = & 180^\circ-\angle BOC \\
& = & 180^\circ-144^\circ \\
& = & 36^\circ
\end{array}$

