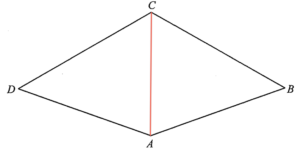
- 由於 $AB=AD$ 及 $BC=CD$,則 $ABCD$ 為一菱形。由此,$AC$ 為 $\angle BAD$ 的角平分線。所以,$\angle BAC = 73^\circ$。
$\begin{array}{rcl}
\angle ACB & = & 180^\circ – 73^\circ – 59^\circ \\
& = & 48^\circ
\end{array}$利用正弦公式於 $\Delta ABC$,可得
$\begin{array}{rcl}
\dfrac{AB}{\sin \angle ACB} & = & \dfrac{BC}{\sin \angle ABC} \\
\dfrac{AB}{\sin 48^\circ} & = & \dfrac{24}{\sin 73^\circ} \\
AB & = & 18.650~410~03 \\
& = & 18.7 \text{ cm}
\end{array}$ -
- 利用餘弦公式於 $\Delta ABD$,可得
$\begin{array}{rcl}
BD^2 & = & AB^2 + AD^2 – 2(AB)(AD)\cos \angle BAD \\
& = & 2(18.650~410~03)^2 -2(18.650~410~03)^2\cos 92^\circ \\
BD & = & 26.831~964~45 \\
& = & 26.8\text{ cm}
\end{array}$ - 在直線 $AC$ 上加上點 $X$,使得 $BX\perp AC$ 及 $DX \perp AC$。
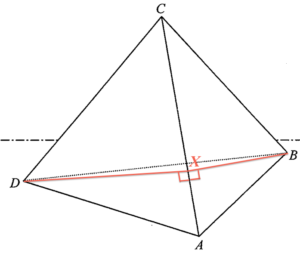
在 $\Delta ABX$ 中,
$\begin{array}{rcl}
\sin BAX & = & \dfrac{BX}{AB} \\
BX & = & 18.650~410~03 \sin 73^\circ \\
& = & 17.835~475~81 \text{ cm}
\end{array}$留意 $BX=DX$。利用餘弦公式於 $\Delta XBD$,可得
$\begin{array}{rcl}
\cos \angle BXD & = & \dfrac{BX^2 + DX^2 – BD^2}{2(BX)(DX)} \\
& = & -0.131~632~845 \\
\angle BXD & = & 97.563~958~43^\circ
\end{array}$所以,所求的角為 $97.6^\circ$。
- 留意 $BD$ 為固定長度,及 $\Delta BPD$ 為一等腰三角形。若等腰三角形的兩腰變長,則其中的夾角會變小。
當動點 $P$ 由點 $A$ 移至點 $X$ 時,$BP$ 的長度會減少。 $\angle BPD$ 會由 $\angle BAD$ 增大至 $\angle BXD$。
由於 $BX$ 為 $B$ 至線段 $AC$ 的最短距離,所以當 $P$ 由點 $X$ 移至點 $C$ 時,$BP$ 的長度會增加。由此,$\angle BPD$ 會由 $\angle BXD$ 變小至 $\angle BCD$。
- 利用餘弦公式於 $\Delta ABD$,可得
2010-I-15
答案:(a) $18.7\text{ cm}$ (b) (i) $26.8\text{ cm}$ (ii) $97.6^\circ$ (iii) $\angle BPD$ 由 $\angle BAD$ 增加至 $\angle BQD$,之後減少至 $\angle BCD$。

