答案:B
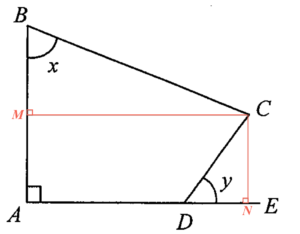

於 $AB$ 上加點 $M$ 使得 $CM\perp AB$,且於 $DE$ 上加點 $N$ 使得 $CN\perp DE$。考慮 $\Delta BCM$,
$\begin{array}{rcl}
\sin x & = & \dfrac{CM}{BC} \\
CM & = & BC \sin x
\end{array}$
考慮 $\Delta CDN$,
$\begin{array}{rcl}
\cos y & = & \dfrac{DN}{CD} \\
DN & = & CD \cos y
\end{array}$
所以,可得
$\begin{array}{rcl}
AD & = & CM – DN \\
& = & BC \sin x – CD \cos y
\end{array}$

