I 為正確。
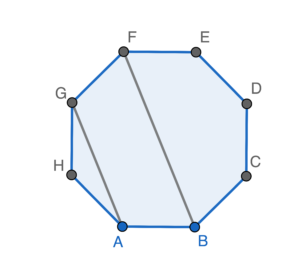
$\begin{array}{rcl}
\angle ABC & = & \dfrac{1}{8}[(8-2) \times 180^\circ ] \\
\angle ABC & = & 135^\circ \\
\angle ABF & = & \dfrac{1}{2} \times \angle ABC \\
\angle ABF & = & 67.5^\circ
\end{array}$
在 $\Delta AHG$ 中,由於 $AH = GH$,$\angle AGH =\angle GAH$ (等腰三角形的底角)。
$\begin{array}{rcll}
\angle GAH & = & \dfrac{1}{2} (180^\circ -\angle AHG) & \text{(三角形的內角和)} \\
\angle GAH & = & \dfrac{1}{2} (180^\circ -135^\circ) \\
\angle GAH & = & 22.5^\circ
\end{array}$
所以,可得
$\begin{array}{rcl}
\angle BAG & = & \angle BAH -\angle GAH \\
\angle BAG & = & 135^\circ -22.5^\circ \\
\angle BAD & = & 112.5^\circ
\end{array}$
由此,可得
$\begin{array}{cl}
& \angle ABF + \angle BAG \\
= & 67.5^\circ +112.5^\circ \\
= & 180^\circ
\end{array}$
所以,$AG\text{//}BF$ (同旁內角互補)。
II 為正確。
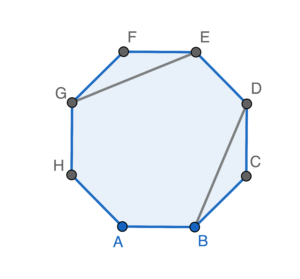
在 $\Delta BCD$ 和 $\Delta EFG$ 中,
$\begin{array}{rcl}
BC & = & EF & \text{(正多邊形的定義)} \\
CD & = & FG & \text{(正多邊形的定義)} \\
\angle BCD & = & \angle EFG & \text{(正多邊形的定義)} \\
\end{array}$
$\therefore \Delta BCD \cong \Delta EFG$ (S.A.S.)。
由此,$BD = EG$ ($\cong \Delta$ 的對應邊)。
III 為正確。
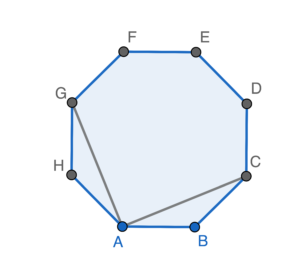
$\begin{array}{rcl}
\angle CAG & = & \angle BAH -\angle BAC -\angle GAH \\
\angle CAG & = & 135^\circ -22.5^\circ -22.5^\circ \\
\angle CAG & = & 90^circ
\end{array}$
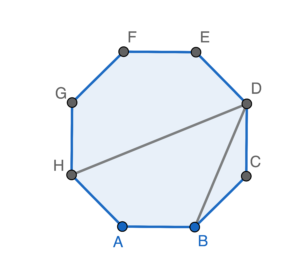
$\begin{array}{rcl}
\angle BDH & = & \dfrac{1}{2} \times \angle CDE -\angle BDC \\
\angle BDH & = & \dfrac{1}{2} \times 135^\circ -22.5^\circ \\
\angle BDH & = & 45^\circ
\end{array}$
由此,$\angle CAG =2\angle BDH$。

