答案:B
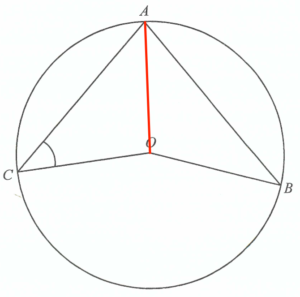

連結 $OA$。
$\begin{array}{rcll}
\angle CAB & = & \dfrac{1}{2} \angle BOC & \text{(圓心角兩倍於圓周角)} \\
\angle CAB & = & \dfrac{1}{2} \times 164^\circ \\
\angle CAB & = & 82^\circ
\end{array}$
在 $\Delta OAB$ 中,
$\begin{array}{rcll}
\because OA & = & OB & \text{(半徑)} \\
\therefore \angle OAB & = & \angle OBA & \text{(等腰三角形的底角)} \\
\angle OAB & = & 36^\circ
\end{array}$
在 $\Delta OCA$ 中,
$\begin{array}{rcll}
\because OA & = & OC & \text{(半徑)} \\
\therefore \angle OCA & = & \angle OAC & \text{(等腰三角形的底角)} \\
\angle OCA & = & \angle CAB -\angle OAB \\
\angle OCA & = & 82^\circ -36^\circ \\
\angle OCA & = & 46^\circ
\end{array}$

