2022-II-25

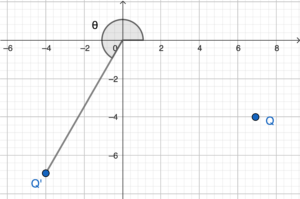
留意變換後的像的直角坐標 $Q’$ 為 $(-4, -4\sqrt{3})$。

$\begin{array}{rcl}
\tan \theta & = & \dfrac{-4\sqrt{3}}{-4} \\
\tan \theta & = & \sqrt{3} \\
\theta & = & 60^\circ \text{ 或 } 240^\circ
\end{array}$

由於 $Q’$ 在象限 III，則 $\theta = 240^\circ$。

$\begin{array}{rcl}
OQ’ & = & \sqrt{(-4)^2 +(-4\sqrt{3})^2} \\
OQ’ & = & 8
\end{array}$

所以，$Q’$ 的極坐標為 $(8, 240^\circ)$。