- 若 $PQ$ 為圓於 $T$ 的切線，則 $OT$ 必定垂直於 $PQ$。
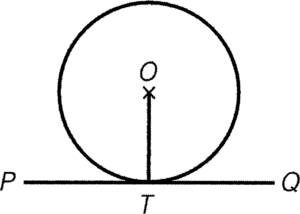
條件：$PQ$ 為 $T$ 上的切線
結論：$OT \perp PQ$
簡記：切線 $\perp$ 半徑
- 若 $OT$ 垂直於 $PTQ$，則 $PQ$ 必定為圓於 $T$ 的切線。
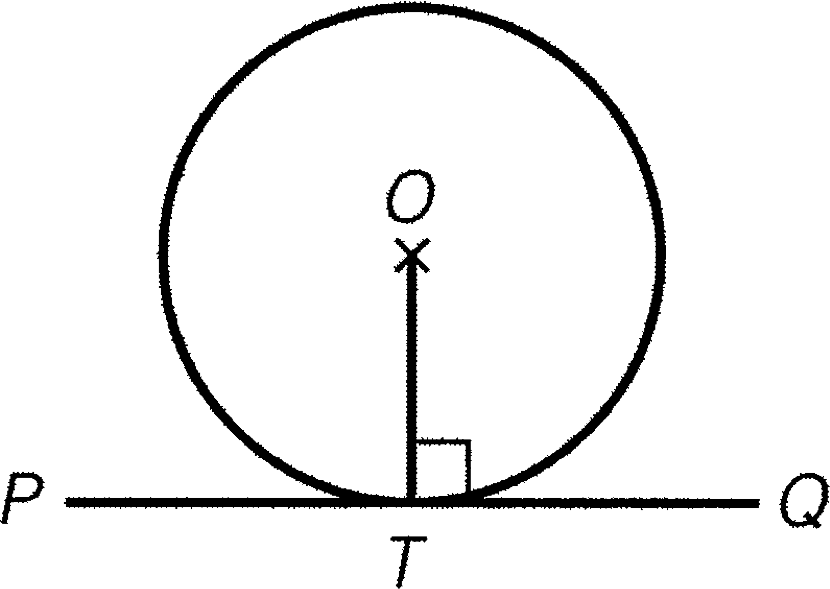
條件：$OT\perp PTQ$
結論：$PQ$ 為切線
簡記：切線 $\perp$ 半徑的逆定理
- 若 $PQ$ 為圓於 $T$ 的切線，則任何通過 $T$ 並垂直於 $PQ$ 的直線必定通過圓心。
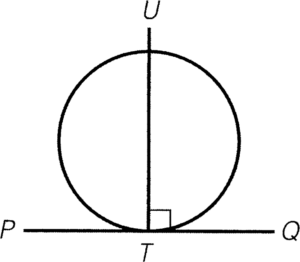
條件：$PQ$ 為圓於 $T$ 的切線，且一垂直線通過 $T$
結論： 該直線必定通過圓心
簡記： $\perp$ 切線同通過切點的直線通過圓心
- 已知 $PT$ 和 $QT$ 為圓的兩切線。則 $\Delta OPT \cong \Delta OQT$。
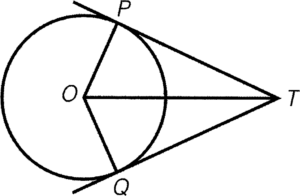
條件：$PT$ 和 $QT$ 均為切線
結論：
- $PT=QT$
- $\angle PTO=\angle QTO$
- $\angle TOP = \angle TOQ$
簡記：切線性質
- 若 $PQ$ 為圓的切線，則內錯弓形上的圓周角必定相等。
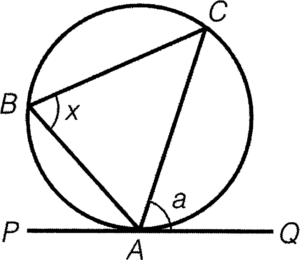
條件：$PQ$ 為切線
結論：$\angle ABC = \angle CAQ$
簡記：內錯弓形上的圓周角
- 若內錯弓形上的圓周角相等，則 $PQ$ 為圓於 $A$ 的切線。
條件：$\angle ABC=\angle CAQ$
結論：$PQ$ 為切線
簡記：內錯弓形上的圓周角的逆定理
Resources for HKDSE Mathematics
