1. Radian Measure – Solving Master

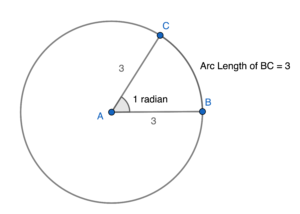
Definition of Radian The measure of an angle subtended at the centre of a circle by an arc equal to its radius is defined as one radian.
Conversion between Degrees and Radians $$\pi\text{ rad}=180^\circ$$
Specical Angles
$$\begin{array}{|c|c|} \hline
\text{Degree} & \text{Radian} \\ \hline
30^\circ & \dfrac{\pi}{6} \\ \hline
45^\circ & \dfrac{\pi}{4} \\ \hline
60^\circ & \dfrac{\pi}{3} \\ \hline
90^\circ & \dfrac{\pi}{2} \\ \hline
120^\circ & \dfrac{2\pi}{3} \\ \hline
135^\circ & \dfrac{3\pi}{4} \\ \hline
150^\circ & \dfrac{5\pi}{6} \\ \hline
180^\circ & \pi \\ \hline
210^\circ & \dfrac{7\pi}{6} \\ \hline
225^\circ & \dfrac{5\pi}{4} \\ \hline
240^\circ & \dfrac{4\pi}{3} \\ \hline
270^\circ & \dfrac{3\pi}{2} \\ \hline
300^\circ & \dfrac{5\pi}{3} \\ \hline
315^\circ & \dfrac{7\pi}{4} \\ \hline
330^\circ & \dfrac{11\pi}{6} \\ \hline
360^\circ & 2\pi \\ \hline
\end{array}
$$