Ans: (a) $0.5\text{ cm}$ (b) $223\text{ cm}^2$ (c) $223\le x< 270$
- The maximum absolute error
$\begin{array}{cl}
= & 1 \div 2 \\
= & 0.5 \text{ cm}
\end{array}$ - Add a point $G$ on $AF$ such that $AF\perp DG$ and $CDG$ is a straight line.
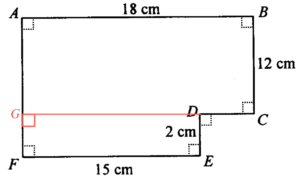
The least possible total area
$\begin{array}{cl}
= & \text{the least possible area of $ABCG$} + \text{the least possible area of $DEFG$} \\
= & 17.5 \times 11.5 + 1.5 \times 14.5 \\
= & 223 \text{ cm}^2
\end{array}$ - The greatest possible total area
$\begin{array}{cl}
= & \text{the greatest possible area of $ABCG$} + \text{the greatest possible area of $DEFG$} \\
= & 18.5 \times 12.5 + 2.5 \times 15.5 \\
= & 270 \text{ cm}^2
\end{array}$Hence, we have $223\le x <270$.

