-
- Since $H$ is the orthocentre of $\Delta ABC$, then $AO\perp BC$. Hence, we have $\angle AOC = 90^\circ$.
Since $BS$ is a diameter of the circle, then we have
$\begin{array}{ll}
\angle BCS = 90^\circ & \text{($\angle$ in semi-circle)}
\end{array}$Consider $AH$ and $SC$,
$\angle AOC + \angle BCS$
$\begin{array}{cl}
= & 90^\circ + 90^\circ \\
= & 180^\circ
\end{array}$$\therefore AH\text{//} SC$ (int. $\angle$s supp.).
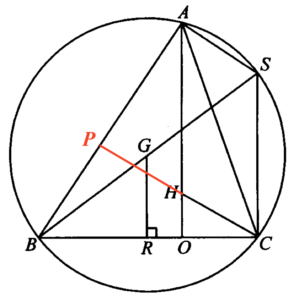
Now, we extend $CH$ to $P$ on $AB$. Since $H$ is the orthocentre of $\Delta ABC$, then $CP \perp AB$. Hence, we have $\angle CPA=90^\circ$.
Since $BS$ is a diameter of the circle, then we have
$\begin{array}{ll}
\angle BAS = 90^\circ & \text{($\angle$ in semi-circle)}
\end{array}$Consider $CH$ and $SA$,
$\angle CPA + \angle BAS$
$\begin{array}{cl}
= & 90^\circ + 90^\circ \\
= & 180^\circ
\end{array}$$\therefore CH\text{//} SA$ (int. $\angle$s supp.).
Since $AH\text{//} SC$ and $CH\text{//} SA$, then $AHCS$ is a parallelogram.
- Given that $G$ is the centre and $GR \perp BC$. Hence, we have
$\begin{array}{ll}
BR = RC & \text{($\perp$ line from centre to chord bisects chord)}
\end{array}$In $\Delta BCS$,
$\begin{array}{ll}
BG = GS & \text{(radii)} \\
BR = RC & \text{(proved)}
\end{array}$$\therefore SC = 2RG$ (mid-pt theorem).
By the result of (a)(i), we have
$\begin{array}{ll}
AH = SC & \text{(opp. sides of //gram)}
\end{array}$Hence, we have $AH=2GR$.
- Since $H$ is the orthocentre of $\Delta ABC$, then $AO\perp BC$. Hence, we have $\angle AOC = 90^\circ$.
-
- Let $x^2 +y^2 +Dx +Ey +F=0$ be the equation of the required circle. Since the circle passes through $A$, $B$ and $C$, then we can substitute the coordinates of $A$, $B$ and $C$ into the equation of the circle. Hence, we have
$\left\{ \begin{array}{l}
(0)^2 + (12)^2 +D(0) + E(12) +F =0 \\
(-6)^2 + (0)^2 +D(-6) + E(0) +F =0 \\
(4)^2 + (0)^2 +D(4) +E(0) +F =0
\end{array}\right.$$\left\{ \begin{array}{ll}
12E + F = -144 & \ldots \unicode{x2460} \\
-6D + F = -36 & \ldots \unicode{x2461} \\
4D + F = -16 & \ldots \unicode{x2462}
\end{array}\right.$$\unicode{x2462} – \unicode{x2461}$, we have
$\begin{array}{rcl}
10D & = & 20 \\
D & = & 2
\end{array}$Sub. $D=2$ into $\unicode{x2462}$, we have
$\begin{array}{rcl}
4(2) + F & = & -16 \\
F & = & -24
\end{array}$Sub. $F=-24$ into $\unicode{x2460}$, we have
$\begin{array}{rcl}
12E + (-24) & = & -144 \\
12E & = & -120 \\
E & = & -10
\end{array}$Therefore, the required equation is $x^2 +y^2 +2x – 10y -24=0$.
- Note that $H$ lies on the positive $y$-axis, let $H=(0,y)$. Since $H$ is the orthocentre of $\Delta ABC$, we have $AB\perp CH$. Hence, we have
$\begin{array}{rcl}
m_{AB} \times m_{CH} & = & -1 \\
\dfrac{12 – 0}{0 – (-6)} \times \dfrac{y-0}{0-4} & = & -1 \\
\dfrac{y}{-2} & = & -1 \\
y & = & 2
\end{array}$Therefore, $H=(0,2)$.
- By the result of (b)(i), $G=(-1,5)$. Consider
$m_{GH} \times m_{BG}$
$\begin{array}{cl}
= & \dfrac{5-2}{-1-0} \times \dfrac{5-0}{-1-(-6)} \\
= & -3 \\
\neq & -1
\end{array}$Therefore $GH\not \perp BG$. Hence, we have $\angle BGH \neq 90^\circ$.
Since $H$ is the orthocentre of $\Delta ABC$, then $HO \perp BC$.
Hence, we have $\angle HOB = 90^\circ$. Therefore, $\angle BGH + \angle HOB \neq 180^\circ$.
Hence, $B$, $O$, $H$ and $G$ are no concyclic.
- Let $x^2 +y^2 +Dx +Ey +F=0$ be the equation of the required circle. Since the circle passes through $A$, $B$ and $C$, then we can substitute the coordinates of $A$, $B$ and $C$ into the equation of the circle. Hence, we have
2006-I-16
Ans: (b) (i) $x^2+y^2+2x-10y-24=0$ (ii) $(0,2)$

