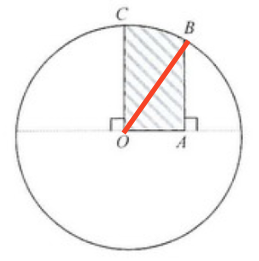
Join $OB$. Since $OC$ and $OB$ are radii, then $OB = 2\text{ cm}$. In $\Delta OAB$,
$\begin{array}{rcl}
\cos \angle BOA & = & \dfrac{OA}{OB} \\
\cos \angle BOA & = & \dfrac{1}{2} \\
\angle BOA & = & 60^\circ
\end{array}$
Hence, we have
$\begin{array}{rcl}
\angle BOC & = & 90^\circ – \angle BOA \\
& = & 30^\circ
\end{array}$
By applying the Pythagoras Theorem to the $\Delta OAB$, we have
$\begin{array}{rcl}
AB^2 & = & OB^2 – OA^2 \\
AB & = & \sqrt{2^2 – 1^2} \\
AB & = & \sqrt{3} \text{ cm}
\end{array}$
Therefore, the area of the shaded region $OABC$
$\begin{array}{cl}
= & \pi (2)^2 \times \dfrac{30^\circ}{360^\circ} + \dfrac{1}{2} \times 1 \times \sqrt{3} \\
= & \left(\dfrac{\pi}{3} + \dfrac{\sqrt{3}}{2} \right) \text{ cm}^2
\end{array}$

