Ans: C
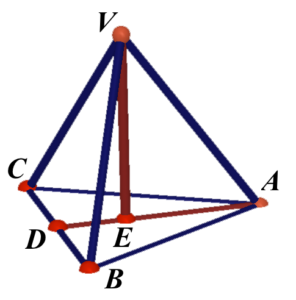

Note that each faces of the tetrahedron are equilateral triangle with side $3\text{ cm}$. Consider the base equilateral triangle $ABC$. Add a point $D$ on $BC$ such that $AD\perp BC$ and $BD=CD$. Note that $E$ is the centroid of $\Delta ABC$.
$\begin{array}{rcl}
AC^2 & = & AD^2 + CD^2 \\
(3)^2 & = & AD^2 + (1.5)^2 \\
AD & = & \dfrac{3\sqrt{3}}{2} \text{ cm}
\end{array}$
Since $E$ is the centroid of $\Delta ABC$, $AE:ED = 2:1$. Hence, we have $AE = \sqrt{3}\text{ cm}$. In $\Delta VEA$,
$\begin{array}{rcl}
VA^2 & = & VE^2 + AE^2 \\
VE^2 & = & (3)^2 – (\sqrt{3})^2 \\
VE^2 & = & 6 \\
VE & = & \sqrt{6} \text{ cm}
\end{array}$
Therefore, the height of the tetrahedron is $\sqrt{6}\text{ cm}$.

