2006-II-47

Ans: B
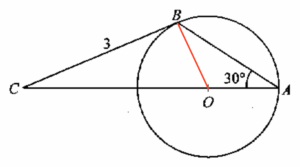
Join $OB$.

In $\Delta OAB$,

$\begin{array}{ll}
OB = BA & \text{(radii)} \\
\angle OBA = \angle OAB & \text{(base $\angle$s, isos. $\Delta$)} \\
\angle OBA = 30^\circ & \\
\end{array}$

$\begin{array}{ll}
\angle BOC = \angle OBA + \angle OAB & \text{(ext. $\angle$ of $\Delta$)} \\
\angle BOC = 30^\circ + 30^\circ & \\
\angle BOC = 60^\circ & \\
\end{array}$

In $\Delta OBC$,

$\begin{array}{ll}
\angle OBC =90^\circ & \text{(radius $\perp$ tangent)}
\end{array}$

Hence, we have

$\begin{array}{rcl}
\tan \angle BOC & = & \dfrac{BC}{OB} \\
\tan 60^\circ & = & \dfrac{3}{OB} \\
OB & = & \dfrac{3}{\tan 60^\circ} \\
OB & = & \sqrt{3}
\end{array}$