2007-I-11

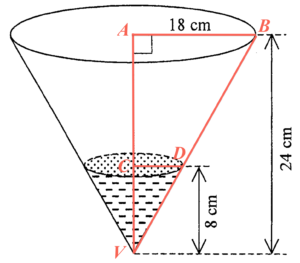
Note that $\Delta VAB \sim \Delta VCD$. Then we have

$\begin{array}{rcl}
\dfrac{VC}{VA} & = & \dfrac{CD}{AB} \\
\dfrac{8}{24} & = & \dfrac{CD}{18} \\
CD & = & 6 \text{ cm}
\end{array}$

Therefore, the base radius of water contained in the vessel is $6\text{ cm}$. Hence, the volume of water contained in the vessel

$\begin{array}{cl}
= & \dfrac{1}{3} \times \pi \times 6^2 \times 8 \\
= & 96\pi \text{ cm}^3
\end{array}$

1. The slant height $VD$ of the water contained in the vessel

   $\begin{array}{cl}
   = & \sqrt{6^2 + 8^2} \\
   = & 10\text{ cm}
   \end{array}$

   Therefore, the area of the wet curved surface of the vessel

   $\begin{array}{cl}
   = & \pi \times 6 \times 19 \\
   = & 60\pi \text{ cm}^2
   \end{array}$

2. Note that the bigger conical vessel is similar to the original one. Therefore the area of the wet curved surface of the bigger vessel is also $60\pi\text{ cm}^2$.