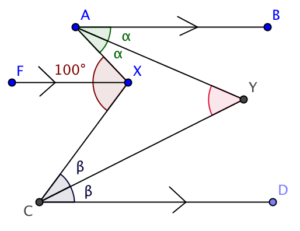
Add a straight line $FX$ such that \\ $AB//FX//CD$. Since $AY$ and $CY$ are the angle bisectors of $\angle BAX$ and $\angle DCX$ respectively, let $\angle BAY = \angle YAX = \alpha$ and $\angle DCY = \angle YCX = \beta$.
Since $AB//FX$, then we have
$\begin{array}{rcl}
\angle AXF & = & \angle BAX \\
\angle AXF & = & 2 \alpha
\end{array}$
Since $FX//CD$, then we have
$\begin{array}{rcl}
\angle FXC & = & \angle XCD \\
\angle FXC & = & 2\beta
\end{array}$
Hence, we have
$\begin{array}{rcl}
\angle AXF + \angle FXC & = & \angle AXC \\
2\alpha + 2\beta & = & 100^\circ \\
2(\alpha + \beta) & = & 100^\circ \\
\alpha + \beta & = & 50^\circ
\end{array}$
Consider polygon $AXCY$,
$\begin{array}{rcl}
\text{reflex }\angle AXC & = & 360^\circ – 100^\circ \\
\text{reflex }\angle AXC & = & 260^\circ
\end{array}$
Since polygon $AXCY$ is a quadrilateral, then we have
$\begin{array}{rcl}
\alpha + 260^\circ + \beta + \angle AYC & = & 360^\circ \\
50^\circ + 260^\circ + \angle AYC & = & 360^\circ \\
\angle AYC & = & 50^\circ
\end{array}$

