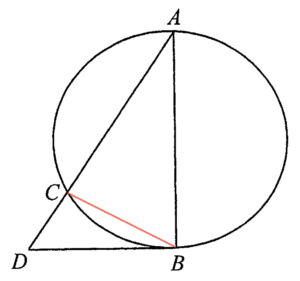
Join $BC$. Consider $\Delta ABD$ and $\Delta ACB$,
$\begin{array}{rcll}
\angle BAD & = & \angle CAB & \text{(common angle)} \\
\angle ACB & = & 90^\circ & \text{($\angle$ in semi-circle)} \\
\angle ABD & = & 90^\circ & \text{(radius $\perp$ tangent)} \\
\therefore \angle ABD & = & \angle ACB \\
\end{array}$
$\begin{array}{rcll}
\angle ADB & = & 180^\circ – \angle BAD – \angle ABD & \text{($\angle$s sum of $\Delta$)} \\
& = & 180^\circ – \angle CAB – \angle ACB & \text{(proved)} \\
& = & \angle ABC & \text{($\angle$s sum of $\Delta$)}
\end{array}$
$\therefore \Delta ABD \sim \Delta ACB$ (A.A.A.).
Therefore, we have
$\begin{array}{rcl}
\dfrac{AD}{AB} & = & \dfrac{AB}{AC} \\
\dfrac{6}{AB} & = & \dfrac{AB}{4} \\
AB^2 & = & 24 \\
AB & = & \sqrt{24} \\
& = & 2\sqrt{6}
\end{array}$

