2008-I-15

$\begin{array}{rcl}
\angle DBH + \angle DHB & = & \angle HDA \\
35^\circ + \angle DHB & = & 50^\circ \\
\angle DHB & = & 15^\circ
\end{array}$

Note that $BD=50\text{ m}$. By applying the sine law to $\Delta BDH$, we have

$\begin{array}{rcl}
\dfrac{BD}{\sin \angle BHD} & = & \dfrac{BH}{\sin BDH} \\
\dfrac{50}{\sin 15^\circ} & = & \dfrac{BH}{\sin (180^\circ-50^\circ)} \\
BH & = & \dfrac{50\sin 130^\circ}{\sin 15^\circ} \\
& = & 147.988~422~3 \\
& \approx & 148 \text{ m}
\end{array}$

1. By applying the cosine law to $\Delta BCH$, we have

   $\begin{array}{rcl}
   \cos \angle CBH & = & \dfrac{BH^2 + BC^2 – CH^2}{2(BH)(BC)} \\
   & = & \dfrac{147.988~422~3^2 + 210^2 – 130^2}{2(147.988~422~3)(210)} \\
   & = & 0.789~968~057 \\
   \angle CBH & = & 37.817~473~47^\circ \\
   & \approx & 37.8^\circ
   \end{array}$

2. 

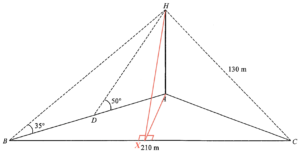
   Add a point $X$ on $BC$ such that $HX \perp BC$ and $AX \perp BC$. Consider $\Delta BXH$,

   $\begin{array}{rcl}
   \sin \angle HBX & = & \dfrac{HX}{BH} \\
   \sin 37.817~473~47^\circ & = & \dfrac{HX}{147.988~422~3} \\
   HX & = & 90.738~804~95 \text{ m}
   \end{array}$

   Consider $\Delta HAB$,

   $\begin{array}{rcl}
   \sin \angle HBA & = & \dfrac{HA}{BH} \\
   \sin 35^\circ & = & \dfrac{HA}{147.988~422~3} \\
   HA & = & 84.882~671~91 \text{ m}
   \end{array}$

   Consider $\Delta HXA$,

   $\begin{array}{rcl}
   \sin \angle HXA & = & \dfrac{HA}{HX} \\
   & = & \dfrac{84.882~671~91}{147.988~422~3} \\
   & = & 0.935~461~646 \\
   \angle HXA & = & 69.302~855~61 \\
   & \approx & 69.3^\circ
   \end{array}$

   Therefore, the required angle is $69.3^\circ$.

3. Note that $HX \perp BC$ and $AX \perp BC$. Therefore, $HX$ is the line of the greatest slope of the plane $HBC$. Hence, the greatest inclined angle on the plane $HBC$ is $\angle HXA$ (i.e. $69.3^\circ$). Therefore, it is impossible to find a point $K$ on $BC$ such that the angle of elevation of $H$ from $K$ is $75^\circ$.