2008-I-17

$\begin{array}{ll}
\angle PAB = \angle PAC & \text{(in-centre)}
\end{array}$

Since $A$, $B$, $P$ and $C$ are four points on the circumference,

$\begin{array}{ll}
\angle PAB = \angle PCB & \text{($\angle$ in the same segment)} \\
\angle PAC = \angle PBC & \text{($\angle$ in the same segment)}
\end{array}$

Hence, we have $\angle PBC = \angle PCB$. Therefore, we have

$\begin{array}{ll}
BP=CP & \text{(sides opp. eq. $\angle$s)}
\end{array}$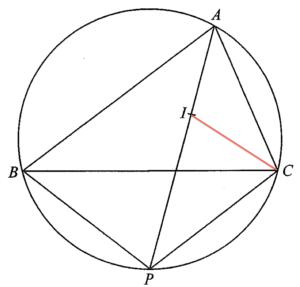

Join $C$ and $I$. Consider $\Delta ABC$,

$\begin{array}{ll}
\angle BCI = \angle ACI & \text{(in-centre)}
\end{array}$

Also, we have

$\begin{array}{ll}
\angle PAC = \angle PCB & \text{(proved)}
\end{array}$

Hence, we have

$\begin{array}{ll}
\angle PCI & \\
= \angle PCB + \angle BCI & \\
= \angle PAC + \angle ACI & \text{(proved)} \\
= \angle PIC & \text{(ext. $\angle$ of $\Delta$)}
\end{array}$

Therefore, we have

$\begin{array}{ll}
CP=IP & \text{(sides opp. eq. $\angle$s)}
\end{array}$

Hence, $BP=CP=IP$.

1. Note that $G$ is the circumcentre of $\Delta ABC$, then $GP$ is the perpendicular bisector of $BC$. Note also that $B$ and $C$ are lying on $x$-axis, then $BC$ is a horizontal line. Hence, the $x$ coordinates of $G$ and $P$ are the same. The $x$ coordinate of $P$

   $\begin{array}{cl}
   = & \dfrac{-80 + 64}{2} \\
   = & -8
   \end{array}$

   Let $P=(-8, y)$. By the result of (a), we have

   $\begin{array}{rcl}
   BP & = & IP \\
   \sqrt{(-80-(-8))^2+(0-y)^2} & = & \sqrt{(0-(-8))^2 + (32-y)^2} \\
   5184 + y^2 & = & 64 + 1024 – 64y +y^2 \\
   64y & = & -4096 \\
   y & = & -64
   \end{array}$

   Therefore, $P=(-8,-64)$. Then, we have

   $\begin{array}{rcl}
   BP & = & \sqrt{(-80-(-8))^2 + (0-(-64))^2} \\
   & = & \sqrt{9280}
   \end{array}$

   Hence, the required equation is

   $\begin{array}{rcl}
   (x-(-8))^2 + (y-(-64))^2 & = & (\sqrt{9280})^2 \\
   x^2 +16x +64 + y^2 + 128y +4096 & = & 9280 \\
   x^2 +y^2 +16x + 128y – 5120 & = & 0
   \end{array}$

2. Let $G=(-8,m)$. Since $G$ is the circumcentre of $\Delta ABC$, then

   $\begin{array}{rcl}
   BG & = & GP \\
   \sqrt{(-80-(-8))^2 + (0-m)^2} & = & m-(-64) \\
   5184 + m^2 & = & (m+64)^2 \\
   5184 + m^2 & = & m^2 +128m +4096 \\
   128m & = & 1088 \\
   m & = & \dfrac{17}{2}
   \end{array}$

   Therefore, $G=(-8,\dfrac{17}{2})$. Note that $PQ$ is a diameter and $G$ is the centre of the circle $ABPC$. Note also that $PQ$ is a vertical line. Hence let $Q=(-8,n)$. Then we have

   $\begin{array}{rcl}
   QG & = & PG \\
   n – \dfrac{17}{2} & = & \dfrac{17}{2} – (-64) \\
   n & = & 81
   \end{array}$

   Therefore, $Q=(-8,81)$.

3. The slope of $BQ$

   $\begin{array}{cl}
   = & \dfrac{81- 0}{-8-(-80)} \\
   = & \dfrac{9}{8}
   \end{array}$

   The slope of $QI$

   $\begin{array}{cl}
   = & \dfrac{81- 32}{-8-0} \\
   = & \dfrac{-49}{8}
   \end{array}$

   Since the slope of $BQ\times$ the slope of $QI \neq -1$, then $\angle BQI \neq 90^\circ$. Hence, $\angle BQI \neq \angle IRC$. Therefore, $B$, $Q$, $I$ and $R$ are not concyclic.