Ans: C
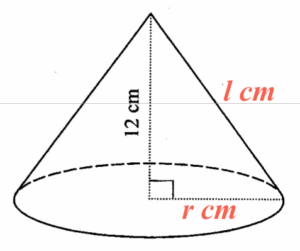

Let $r\text{ cm}$ and $l \text{ cm}$ be the base radius and the slant height respectively. Since the circumference of the base is $18\pi\text{ cm}$, we have
$\begin{array}{rcl}
2 \pi r & = & 18 \pi \\
r & = & 9
\end{array}$
By applying the Pythagoras Theorem to the cone, we have
$\begin{array}{rcl}
l^2 & = & 12^2 + r^2 \\
l & = & \sqrt{144 + 9^2} \\
& = & 15
\end{array}$
Therefore, the surface area of the circular cone
$\begin{array}{cl}
= & \pi \times (9) \times (15) + \pi \times (9)^2 \\
= & 216 \pi \text{ cm}^2
\end{array}$

