Ans: B
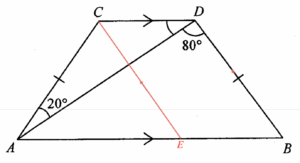

Let $\angle ADC = y$. Add a point $E$ on $AB$ such that $EC//BD$. Note that $CEBD$ is a parallelogram, then we have
$\begin{array}{rcl}
\angle CEB & = & \angle CDB \\
& = & y + 80^\circ
\end{array}$
Since $AEB$ is a straight line, we have
$\begin{array}{rcl}
\angle CEA & = & 180^\circ – \angle CEB \\
& = & 180^\circ – (y+80^\circ) \\
& = & 100^\circ – y
\end{array}$
Since $CD//AB$, then $\angle DAB = y$.
Since $CEBD$ is a parallelogram, then we have $EC = BD$. Therefore, $AC = EC$. Hence, we have
$\begin{array}{rcl}
\angle CAE & = & \angle CEA \\
y + 20^\circ & = & 100^\circ – y \\
2y & = & 80^\circ \\
y & = & 40^\circ
\end{array}$

