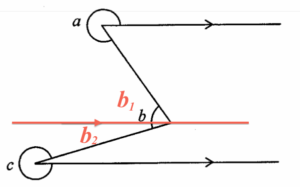
Add a horizontal line and the line divides $b$ into $b_1$ and $b_2$. Refer to the above figure. By the property of parallel lines, we have $a+b_1=360^\circ$ and $c+b_2=360^\circ$.
A may be false. Suppose $a=315^\circ$, $b_1=45^\circ$, $b_2=15^\circ$ and $c=345^\circ$. It is clear that $a+b_1=360^\circ$ and $c+b_2=360^\circ$, but $a+b \neq c$.
B may be false. Suppose $a=315^\circ$, $b_1=45^\circ$, $b_2=15^\circ$ and $c=345^\circ$. It is clear that $a+b_1=360^\circ$ and $c+b_2=360^\circ$, but $a+b \neq c+ 90^\circ$.
C may be false. Suppose $a=315^\circ$, $b_1=45^\circ$, $b_2=15^\circ$ and $c=345^\circ$. It is clear that $a+b_1=360^\circ$ and $c+b_2=360^\circ$, but $a+c \neq b + 540^\circ$.
D must be true. Since $a+b_1=360^\circ$ and $c+b_2=360^\circ$, we have
$\begin{array}{rcl}
(a +b_1) + (c+b_2) & = & 360^\circ + 360^\circ \\
a + (b_1 + b_2) + c & = & 720^\circ \\
a + b + c & = & 720^\circ
\end{array}$

