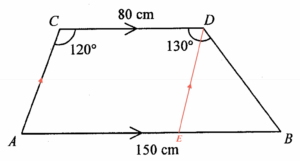
Add a point $E$ on $AB$ such that $AC//ED$. Then $AEDC$ is a parallelogram. Since $AC // ED$, we have
$\begin{array}{rcl}
\angle ACD + \angle CDE & = & 180^\circ \\
120^\circ + \angle CDE & = & 180^\circ \\
\angle CDE & = & 60^\circ
\end{array}$
Since $CD//AB$, we have
$\begin{array}{rcl}
\angle DEB & = & \angle CDE \\
& = & 60^\circ
\end{array}$
Since $AEDC$ is a parallelogram, then $AE=CD$. Hence, we have
$\begin{array}{rcl}
EB & = & AB – AE \\
& = & 150 – 80 \\
& = & 70\text{ cm}
\end{array}$
Consider $\Delta BED$,
$\begin{array}{rcl}
\angle EDB & = & 130^\circ – \angle CDE \\
& = & 130^\circ – 60^\circ \\
& = & 70^\circ
\end{array}$
Hence by applying the sine law to $\Delta BED$, we have
$\begin{array}{rcl}
\dfrac{BD}{\sin \angle BED} & = & \dfrac{EB}{\sin \angle EDB} \\
\dfrac{BD}{\sin 60^\circ} & = & \dfrac{70}{\sin70^\circ} \\
BD & = & \dfrac{70\sin 60^\circ}{\sin 70^\circ} \\
& = & 64.512~348~96 \\
& \approx & 65\text{ cm}
\end{array}$

