Ans: D
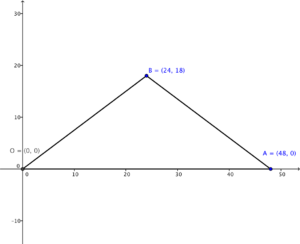

Note that $x=24$ is a vertical line passes through point $B$ and perpendicular to $OA$. Therefore, the orthocentre of $\Delta ABO$ lies on $x=24$. Then let $G=(24,y)$ be the coordinates of the orthocentre of $\Delta ABO$. Since $AG \perp OB$, we have
$\begin{array}{rcl}
m_{AG} \times m_{OB} & = & -1 \\
\dfrac{0-y}{48-24} \times \dfrac{18-0}{24-0} & = & -1 \\
-18y & = & -576 \\
y & = & 32
\end{array}$

