2009-I-13

$\begin{array}{cl}
= & \dfrac{1}{3} \times \pi (12)^2 \times 18 \\
= & 864\pi \text{ cm}^3
\end{array}$

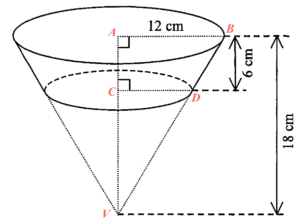
Since $\Delta VAB \sim \Delta VCD$, then we have

$\begin{array}{rcl}
\dfrac{VA}{VC} & = & \dfrac{AB}{CD} \\
\dfrac{18}{18-6} & = & \dfrac{12}{CD} \\
CD & = & 8\text{ cm}
\end{array}$

Therefore, the volume of the frustum

$\begin{array}{cl}
= & 864\pi – \dfrac{1}{3}\times \pi (8)^2 \times 12 \\
= & 608\pi \text{ cm}^3
\end{array}$

$\begin{array}{cl}
= & \pi (8)^2 \times 10 \\
= & 640\pi \text{ cm}^3
\end{array}$

Therefore, the volume of the water in the frustum on the top

$\begin{array}{cl}
= & 884\pi – 640 \pi \\
= & 244 \pi \text{ cm}^3
\end{array}$

Since the frustum at the top and the frustum formed by the water are not similar, we have to consider the original right circular conical container.

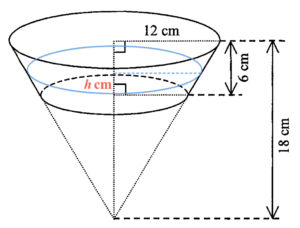
Since the whole conical container is similar to the water in the frustum on the top plus the lower part of the container, which is cut off in part (a)(ii), then we have

$\begin{array}{rcl}
\dfrac{\text{capacity of the container}}{\text{volume of water and the lower part}} & = & \left(\dfrac{18}{12 + h} \right)^3 \\
\dfrac{864\pi}{244 + \frac{1}{3} \times \pi (8)^2 \times 12} & = & \left(\dfrac{18}{12+h}\right)^3 \\
\dfrac{864\pi}{500\pi} & = & \left(\dfrac{18}{12+h} \right)^3 \\
\dfrac{6}{5} & = & \dfrac{18}{12+h} \\
12 + h & = & 18 \times \dfrac{6}{5} \\
12 + h & = & 15 \\
h & = & 3
\end{array}$

Therefore, the depth of water in the frustum at the top is $3\text{ cm}$. Hence, the depth of water in the vessel

$\begin{array}{cl}
= & 10 + 3 \\
= & 13\text{ cm}
\end{array}$

$\begin{array}{cl}
= & 608\pi – 244 \pi \\
= & 364 \pi \\
= & 1~143.539~726 \text{ cm}^3 \\
> & 1~000 \text{ cm}^3
\end{array}$

Therefore, the water will not overflow.