Ans: B
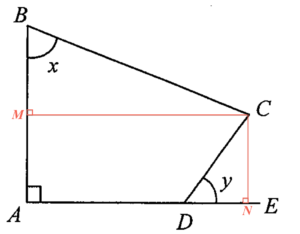

Add a point $M$ on $AB$ such that $CM\perp AB$, and add a point $N$ on $DE$ such that $CN\perp DE$. Consider $\Delta BCM$,
$\begin{array}{rcl}
\sin x & = & \dfrac{CM}{BC} \\
CM & = & BC \sin x
\end{array}$
Consider $\Delta CDN$,
$\begin{array}{rcl}
\cos y & = & \dfrac{DN}{CD} \\
DN & = & CD \cos y
\end{array}$
Therefore, we have
$\begin{array}{rcl}
AD & = & CM – DN \\
& = & BC \sin x – CD \cos y
\end{array}$

