Ans: C
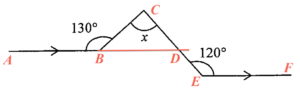

The extension of $AB$ intersects $CE$ at $D$. Since $ABD$ is a straight line, we have
$\begin{array}{rcl}
\angle CBD & = & 180^\circ – 130^\circ \\
& = & 50^\circ
\end{array}$
Since $AD//EF$, we have
$\begin{array}{rcl}
\angle BDE & = & \angle DEF \\
& = & 120^\circ
\end{array}$
Consider $\Delta BCD$, we have
$\begin{array}{rcl}
\angle CBD + \angle BCD & = & \angle BDE \\
50^\circ + x & = & 120^\circ \\
x & = & 70^\circ
\end{array}$

