Ans: B
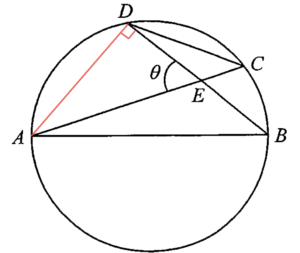

Join $AD$. Since $AB$ is a diameter of the circle $ABCD$, then $\angle ADB = 90^\circ$. Consider $\Delta ADE$, we have $\cos\theta =\dfrac{DE}{AE}$.
Consider $\Delta ABE$ and $\Delta DCE$,
$\begin{array}{ll}
\angle AEB = \angle DEC & \text{(vert. opp. $\angle$s)} \\
\angle EAB = \angle EDC & \text{($\angle$s in the same segment)} \\
\angle EBA = \angle ECD & \text{($\angle$s in the same segment)}
\end{array}$
Therefore, $\Delta ABE \sim \Delta DCE$ (AAA). Hence, we have
$\begin{array}{rcl}
\dfrac{CD}{AB} & = & \dfrac{DE}{AE} \\
& = & \cos \theta
\end{array}$

