Ans: C
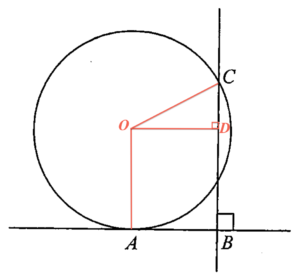

Denote $O$ the centre of the circle. Add a perpendicular line from the centre $O$ to $BC$, and denote $D$ the intersection point. Let $r$ be the radius of the circle. Note that $OA = BD = OC = r$ and $OD = AB = 20$. By applying the Pythagoras Theorem to $\Delta OCD$, we have
$\begin{array}{rcl}
OC^2 & = & OD^2 + CD^2 \\
r^2 & = & 20^2 + (50-r)^2 \\
r^2 & = & 400 + 2500-100r +r^2 \\
100r & = & 2900 \\
r & = & 29
\end{array}$

