Ans: (a) $126^\circ$
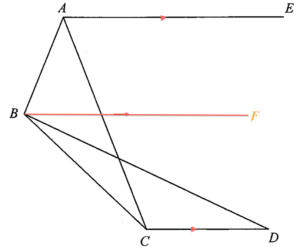
Add a straight line $BF$ such that $AE//BF//CD$ as shown in the above figure.
- Since $AE//BF$, then
$\begin{array}{rcl}
\angle BAE + \angle ABF & = & 180^\circ \\
108^\circ + \angle ABF & = & 180^\circ \\
\angle ABF & = & 72^\circ
\end{array}$Since $BF//CD$, then
$\begin{array}{rcl}
\angle CBF + \angle BCD & = & 180^\circ \\
\angle CBD + 126^\circ & = & 180^\circ \\
\angle CBD & = & 54^\circ
\end{array}$Hence, we have
$\begin{array}{rcl}
\angle ABC & = & \angle ABF + \angle CBF \\
& = & 72^\circ + 54^\circ \\
& = & 126^\circ
\end{array}$ - In $\Delta ABC$ and $\Delta DCB$,
$\begin{array}{ll}
BC = CB & \text{(Common side)} \\
AB = DC & \text{(Given)} \\
\angle ABC = \angle BCD = 126^\circ & \text{(Proved)}
\end{array}$$\therefore \Delta ABC \cong \Delta DCB$. (S.A.S)
