2010-I-15

$\begin{array}{rcl}
\angle ACB & = & 180^\circ – 73^\circ – 59^\circ \\
& = & 48^\circ
\end{array}$

By applying the sine law to $\Delta ABC$, we have

$\begin{array}{rcl}
\dfrac{AB}{\sin \angle ACB} & = & \dfrac{BC}{\sin \angle ABC} \\
\dfrac{AB}{\sin 48^\circ} & = & \dfrac{24}{\sin 73^\circ} \\
AB & = & 18.650~410~03 \\
& = & 18.7 \text{ cm}
\end{array}$

1. By applying the cosine law to $\Delta ABD$, we have

   $\begin{array}{rcl}
   BD^2 & = & AB^2 + AD^2 -2(AB)(AD)\cos \angle BAD \\
   & = & 2(18.650~410~03)^2 -2(18.650~410~03)^2\cos 92^\circ \\
   BD & = & 26.831~964~45 \\
   & = & 26.8\text{ cm}
   \end{array}$

2. Adding a point $X$ on $AC$ such that $BX\perp AC$ and $DX \perp AC$.
   

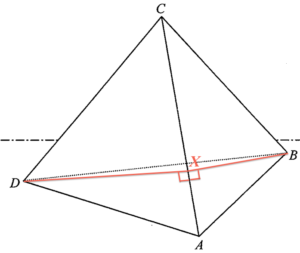
   In $\Delta ABX$,

   $\begin{array}{rcl}
   \sin BAX & = & \dfrac{BX}{AB} \\
   BX & = & 18.650~410~03 \sin 73^\circ \\
   & = & 17.835~475~81 \text{ cm}
   \end{array}$

   Note that $BX=DX$. By applying cosine law to $\Delta XBD$, we have

   $\begin{array}{rcl}
   \cos \angle BXD & = & \dfrac{BX^2 + DX^2 – BD^2}{2(BX)(DX)} \\
   & = & -0.131~632~845 \\
   \angle BXD & = & 97.563~958~43^\circ
   \end{array}$

   Therefore, the required angle is $97.6^\circ$.

3. Note that $BD$ is constant, and $\Delta BPD$ is an isosceles triangle. The longer the two equal sides, the smaller the included angle.

   When the moving point $P$ moves from $A$ to $X$, the length of $BP$ becomes shorter. Hence $\angle BPD$ increases from $\angle BAD$ to $\angle BXD$.

   Since $BX$ is the shortest distance from $B$ to the line segment $AC$, then when $P$ moves from $X$ to $C$, $BP$ becomes longer. Hence $\angle BPD$ decreases from $\angle BXD$ to $\angle BCD$.