Ans: A
Denote $O$ the centre of the semi-circle and join $OD$. Note that the radius of the semi-circle is $13\text{ cm}$.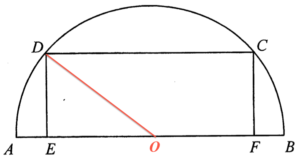
Denote $O$ the centre of the semi-circle and join $OD$. Note that the radius of the semi-circle is $13\text{ cm}$.

$\begin{array}{rcl}
OE & = & OA – AE \\
& = & 13 – 1 \\
& = & 12 \text{ cm}
\end{array}$
Since $CDEF$ is a rectangle, $\angle DEO = 90^\circ$. Then by the Pythagoras Theorem, we have
$\begin{array}{rcl}
DE & = & \sqrt{OD^2 – OE^2} \\
& = & \sqrt{13^2 – 12^2} \\
& = & 5 \text{ cm}
\end{array}$
Therefore, the area of the rectangle $CDEF$
$\begin{array}{cl}
= & DE \times EF \\
= & 5 \times 2 \times OE \\
= & 5 \times 2 \times 12 \\
= & 120 \text{ cm}^2
\end{array}$

