Denote $O$ the centre of the circle $ABCD$ and $Z$ the mid-point of $BC$. Hence, $OZ \perp BC$. Refer to the following figure.
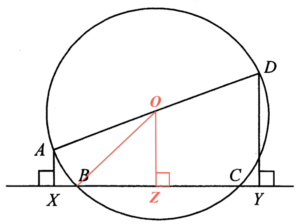
Note that $OB=OA= 10\text{ cm}$ and $BZ = ZC = 6 \text{ cm}$. By applying the Pythagoras Theorem to $\Delta OBZ$, we have
$\begin{array}{rcl}
OZ^2 & = & OB^2 – BZ^2 \\
OZ & = & \sqrt{10^2 – 6^2} \\
& = & 8\text{ cm}
\end{array}$
Since $AO=OD$ and $AX//OZ//DY$, then by the intercept theorem, we have $XZ = ZY$.
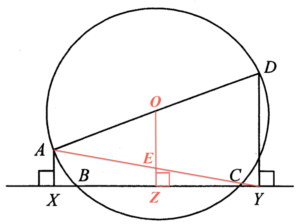
Join $AY$ and denote $E$ the intersection point of $AY$ and $OZ$. Consider $\Delta ADY$. Since $AO=OD$ and $OE//DY$, then by the intercept theorem, $AE = EY$. Since $AO=OD$ and $AE = EY$, then by the mid-point theorem, $DY = 2OE$.
Consider $\Delta AXY$. Since $AE = EY$ and $XZ = ZY$, then by the mid-point theorem, $AX = 2 EZ$. Hence, we have
$\begin{array}{rcl}
AX + DY & = & 2 EZ + 2 OE \\
& = & 2 (OE + EZ) \\
& = & 2 OZ \\
& = & 2 \times 8 \\
& = & 16 \text{ cm}
\end{array}$

