2011-II-49

Ans: C
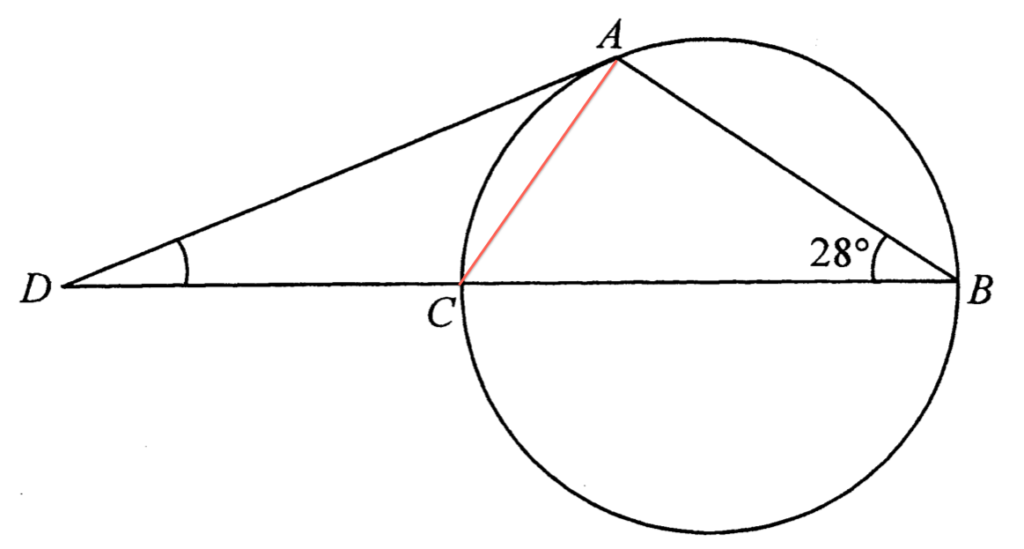
Join $AC$.

Since $DA$ is the tangent to the circle at $A$, then

$\begin{array}{rcl}
\angle DAC & = & \angle ABC \\
& = & 28^\circ
\end{array}$

Since $BC$ is a diameter of the circle, then $\angle CAB = 90^\circ$. Hence, we have

$\begin{array}{rcl}
\angle ACD & = & \angle CAB + \angle ABC \\
& = & 90^\circ + 28^\circ \\
& = & 118^\circ
\end{array}$

In $\Delta ACD$,

$\begin{array}{rcl}
\angle ADB & = & 180^\circ – \angle ACD -\angle DAC \\
& = & 180^\circ – 118^\circ – 28^\circ \\
& = & 34^\circ
\end{array}$