Ans: $19^\circ$
$\because AB//OC$,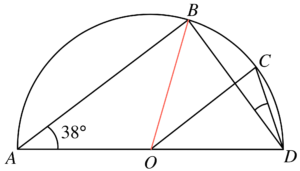
$\because AB//OC$,
$\begin{array}{rcl}
\angle COD & = & \angle BAD \\
& = & 38^\circ
\end{array}$
Join $OB$.

$\because OA \mbox{ and } OB$ are radius,
$\begin{array}{rcl}
\angle OBA & = & \angle OAB \\
& = & 38^\circ
\end{array}$
In $\Delta OAB$,
$\begin{array}{rcl}
\angle OAB+\angle OBA & = & \angle BOD \\
38^\circ+38^\circ & = & \angle BOC+\angle COD \\
\angle BOC+38^\circ & = & 76^\circ \\
\angle BOC & = & 38^\circ
\end{array}$
Hence, we have
$\begin{array}{rcl}
\angle BDC & = & \dfrac{1}{2} \angle BOC \\
& = & \dfrac{1}{2} \times 38^\circ \\
& = & 19^\circ
\end{array}$

