2011SP-I-19

1. Join $CD$.
   

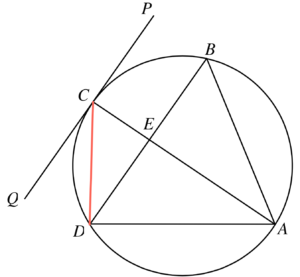
   $\angle QCD = \angle CDE$ (alt. $\angle$s, $PQ//BD$)

   $\angle QCD = \angle DAE$ ($\angle$ in alt. seg.)

   $\angle CDE= \angle BAE$ ($\angle$ in the same seg.)

   $\therefore \angle DAE = \angle BAE$.

   $AD=AB$ (given)

   $AE=AE$ (common side)

   $\therefore \Delta ABD\cong \Delta ADE$ (S.A.S.)

2. $\because BE = DE$ (corr. sides, $\cong \Delta$)

   $\therefore AE$ is a median.

   $\therefore$ the centroid is on $AE$.

   $\because \angle BAE = \angle DEA$ (proved)

   $\therefore AE$ is the angle bisector of $\angle BAD$.

   $\therefore$ the circumcenter is on $AE$.

   $\because \angle AEB = \angle AED$ (corr. $\angle$s, $\cong \Delta$)

   $\therefore AE \perp BD$

   $\therefore AE$ is an altitude of $\Delta ABD$.

   $\therefore$ the orthocentre is on $AE$.

   $\because AE \perp BD$ and $BE=DE$,

   $\therefore AE$ is the perpendicular bisector of $BD$.

   $\therefore$ the in-centre is on $AE$.

   $\therefore$ the in-centre, the orthocentre, the centroid and the circumcenter of $\Delta ABD$ are collinear.

$\left\{ \begin{array}{l}
14^2+4^2+14D+4E+F=0 \\
8^2+12^2+8D+12E+F=0 \\
4^2+4^2+4D+4E+F=0 \\
\end{array} \right.$

After simplifying, we have

$\left\{ \begin{array}{ll}
14D+4E+F=-212 & \ldots \unicode{x2460} \\
8D+12E+F=-208 & \ldots \unicode{x2461} \\
4D+4E+F = -32 & \ldots \unicode{x2462}
\end{array} \right.$

$\unicode{x2460} – \unicode{x2462}$, we have

$\begin{array}{rcl}
10D & = & -180 \\
D & = & -18
\end{array}$

$\unicode{x2461} – \unicode{x2462}$, we have

$\begin{array}{rcl}
4D+8E & = & -176 \\
E & = & -13 \\
\end{array}$

Sub. $D=-18$ and $E=-13$ into $\unicode{x2462}$, we have

$\begin{array}{rlc}
4(-18)+4(-13)+F & = & -32 \\
F & = & 92 \\
\end{array}$

$\therefore$ the equation of the circle is $x^2+y^2-18x-13y+92=0$.

Since $PQ//BD$, their slopes are the same.

The slope of $PQ$

$\begin{array}{cl}
= & \mbox{The slope of }BD \\
= & \dfrac{12-4}{8-4} \\
= & 2
\end{array}$

Let $y=2x+c$ be the equation of $PQ$.

$\left\{ \begin{array}{ll}
x^2+y^2-18x-13y+92=0 & \ldots \unicode{x2463}\\
y=2x+c & \ldots \unicode{x2464}
\end{array} \right.$

Sub. $\unicode{x2464}$ into $\unicode{x2463}$, we have

$\begin{array}{rcl}
x^2+(2x+c)^2-18x-13(2x+c)+92 & = & 0 \\
5x^2+(4c-44)x +(c^2-13c+92) & = & 0
\end{array}$

Since $PQ$ is a tangent to the circle, then

$\begin{array}{rcl}
\Delta & = & 0 \\
(4c-44)^2-4(5)(c^2-13c+92) & = & 0 \\
c^2+23c -24 & = & 0 \\
(c-1)(c+24) & = & 0
\end{array}$

$\therefore c=1$ or $c=-24$ (rejected).

$\therefore$ the equation of $PQ$ is $y=2x+1$.