Let $O$ be the centre of the circle. Join $OD$ and $OC$.
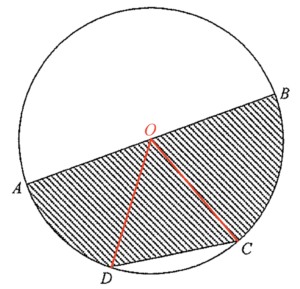
Note that $OA$, $OB$, $OC$ and $OD$ are radii and the radius is $6 \mbox{ cm}$. Therefore, $\Delta OCD$ is an equilateral triangle. And hence $\angle COD = 60^\circ$.
Therefore, the area of $\Delta OCD$
$\begin{array}{cl}
= & \dfrac{1}{2} (6)(6)\sin 60^\circ \\
= & 9\sqrt{3} \mbox{ cm}^2
\end{array}$
Note also that
$\begin{array}{rcl}
\angle AOD+\angle BOC & = & 180^\circ – \angle COD \\
& = & 180^\circ-60^\circ \\
& = & 120^\circ
\end{array}$
Then, the sum of the areas of sectors $OAD$ and $OBC$
$\begin{array}{cl}
= & \pi(6)^2\times\dfrac{\angle AOD}{360^\circ}+\pi(6)^2\times\dfrac{\angle BOC}{360^\circ} \\
= & \pi(6)^2\times\dfrac{\angle AOD+\angle BOC}{360^\circ} \\
= & \pi(6)^2\times \dfrac{120^\circ}{360^\circ} \\
= & 12\pi \mbox{ cm}^2 \\
\end{array}$
Therefore, the area of the shaded region $=(12\pi + 9\sqrt{3}) \mbox{ cm}^2$.

