- In $\Delta ABC$, by cosine law we have
$\begin{array}{rcl}
AB^2 & = & AC^2+BC^2-2(AC)(BC)\cos \angle ACB \\
& = & (20)^2+(12)^2-2(20)(12)\cos 60^\circ \\
AB & = & \sqrt{304} \\
& = &17.435~595~77\mbox{ cm}
\end{array}$ - Add a point $X$ on $AB$ such that $CX\perp AB$.
Note that $\Delta ABC \cong \Delta ABD$. Therefore $CX=DX$ and $DX\perp AB$.
Hence, the required angle is $\angle CXD$.
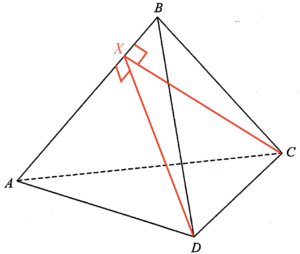
Consider the area of $\Delta ABC$,
$\begin{array}{rcl}
\dfrac{1}{2}(AB)(CX) & = & \dfrac{1}{2}(BC)(AC)\sin \angle ABC \\
(\sqrt{304})(CX) & = & (12)(20)\dfrac{\sqrt{3}}{2} \\
CX & = & 11.920~791~21\mbox{ cm}
\end{array}$In $\Delta CXD$, by cosine law we have
$\begin{array}{rcl}
\cos \angle CXD & = & \dfrac{CX^2+DX^2-CD^2}{2(CX)(DX)} \\
\cos \angle CXD & = & 0.310~370~370\\
\angle CXD & = & 71.918~447~86^\circ
\end{array}$Therefore, the required angle is $71.9^\circ$.
- Since $CX\perp AB$, $CX$ is the shortest distance from $C$ to $AB$. Therefore $CP \ge CX$. Hence, we have
$\begin{array}{rcl}
\cos \angle CXD & = &\dfrac{CX^2+DX^2-CD^2}{2(CX)(DX)} \\
& \le & \dfrac{CP^2+DP^2-CD^2}{2(CP)(DP)} \\
& = & \cos \angle CPD
\end{array}$$\therefore \angle CXD \ge \angle CPD$.
Therefore when $P$ moves from $A$ to $X$, $\angle CPD$ increases.
When $P$ moves from $X$ to $B$, $\angle CPD$ decreases.
2012PP-I-18
Ans: (a) $17.4\text{ cm}$ (b) $71.9^\circ$ (c) When $P$ moves from $A$ to $X$, $\angle CPD$ increases. When $P$ moves from $X$ to $B$, $\angle CPD$ decreases.

