Since $\Delta CEF \sim \Delta DAF$ with $DF=2CF$, then we have
$\begin{array}{rcl}
\dfrac{\mbox{area of }\Delta DAF}{\mbox{area of }\Delta CEF} & = & \left( \dfrac{DF}{CF}\right)^2 \\
\mbox{area of }\Delta DAF & = & 2 \mbox{ cm}^2
\end{array}$
Since $DF=2CF$, then $CD=3CF$.
Note that $ABCD$ is a rectangle. Then $CD=AB$. Hence, $AB=3CF$.
Since $\Delta CEF$ and $\Delta BEA$ have equal base length, then we have
$\begin{array}{rcl}
\dfrac{\mbox{area of }\Delta CEF}{\mbox{area of }\Delta BEA} & = & \dfrac{CF}{BA} \\
\mbox{area of }\Delta BEA & = & 3\mbox{ cm}^2
\end{array}$
Join $AC$.
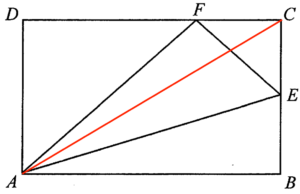
Since $\Delta ACE$ and $\Delta ABE$ have equal base length and height, then their areas are the same.
Hence, the area of $\Delta ABC=6\mbox{ cm}^2$.
Therefore, the area of the rectangle $ABCD$ is $12\mbox{ cm}^2$.
Hence, the area of $\Delta AEF$
$\begin{array}{cl}
= & 12 – 4 – 1 – 3 \\
= & 4 \mbox{ cm}^2
\end{array}$

