In $\Delta ABE$,
$\because AB=AE$,
$\therefore \angle ABE = \angle AEB$.
$\begin{array}{rcl}
\angle ABE & = & \dfrac{1}{2}(180^\circ-112^\circ) \\
& = & 34^\circ
\end{array}$
Produce $DA$ so that $DA$ intersects $BE$ at $G$.
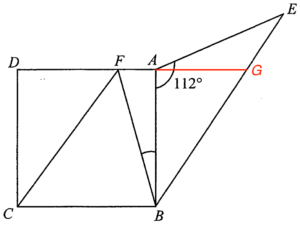
Note that $FG//CB$ and $CF//BE$, therefore $BCFG$ is a parallelogram.
In $\Delta ABG$,
$\begin{array}{rcl}
\tan 34^\circ & = & \dfrac{AG}{AB} \\
AG & = & AB\tan 34^\circ
\end{array}$
Since $AB=BC$ and $BC=FG$, then $AB=FG$.
Hence in $\Delta ABF$, we have
$\begin{array}{rcl}
AF & = & FG-AG \\
& = & AB – AG \\
& = & AB – AB\tan34^\circ \\
& = & AB(1-\tan34^\circ)
\end{array}$
Therefore, we have
$\begin{array}{rcl}
\tan \angle ABF & = & \dfrac{AF}{AB} \\
& = & \dfrac{AB(1-\tan34^\circ)}{AB} \\
& = & 1-\tan34^\circ \\
\angle ABF & = & 18.029~627~8^\circ
\end{array}$

