Ans: C
Let $AD=AF=r\mbox{ cm}$.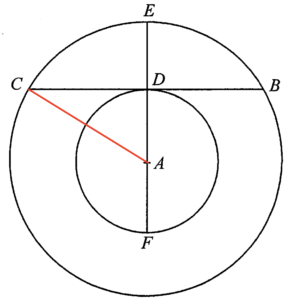
Let $AD=AF=r\mbox{ cm}$.
Since $AD$ is a radius of the smaller circle and $BC$ is the tangent at $D$ to the smaller circle, then $\angle ADC=90^\circ$.
Therefore $D$ is the mid-point of the chord $BC$. Hence, $CD=12\mbox{ cm}$.
Join $A$ and $C$.

Note that $AE$ and $AC$ are radii of the larger circle. Then $AC=AE=(r+8)\mbox{ cm}$.
In $\Delta ACD$,
$\begin{array}{rcl}
AC^2 & = & AD^2 + CD^ 2 \\
(r+8)^2 & = & r^2 + 12^2 \\
16r & = & 80 \\
r & = & 5
\end{array}$
Therefore, we have
$\begin{array}{rcl}
EF & = & ED + DA + AF \\
& = & 8 + 5 + 5 \\
& = & 18 \mbox{ cm}
\end{array}$

